Definitii:
O functie f, reala, de argument real, definita pe D si cu valori in R, este continuă în
punctul a din D, dacă pentru oricare şir (xn), xn din D, convergent la a, sirul (f(xn)) este
convergent şi

Fie f:(D\{a}) - > R o functie reala de variabila reala, unde a este un punct de
acumulare al multimii D (adica in orice vecinatate a lui a se gaseste cel putin un
element din D, diferit de a).
Daca functia f are limita finita in a si
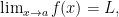
functia
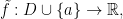
definita prin

evident continua in a, se numeste prelungirea prin continuitate a functiei f in punctul a.
Functii cu proprietatea lui Darboux:
Fie f:I - > R o functie, unde I este un interval inclus in R.
Functia f are proprietatea lui Darboux pe I, daca pentru orice a, b din I, si orice
λ intre f(a) si f(b), exista xλ € (a,b), astfel incat f(xλ) = λ.
Teorema:
Orice functie continua pe un interval are proprietatea lui Darboux pe acel interval.
Teorema lui Weierstrass:
Fie intervalul [a,b] inclus in R; orice functie continua f:[a,b] - > R este marginita si isi
atinge marginile pe acest interval (adica f([a,b]) este un interval inchis si marginit).
O functie f, reala, de argument real, definita pe D si cu valori in R, este continuă în
punctul a din D, dacă pentru oricare şir (xn), xn din D, convergent la a, sirul (f(xn)) este
convergent şi
- Punctul a din D se numeste punct de continuitate al functiei f, daca functia este continua in a.
- Daca functia nu este continua in punctul a, ea se numeste discontinua in punctul a, iar punctul a se numeste punct de discontinuitate al functiei f.
- Daca punctul a este punct de discontinuitate al functiei f, iar f(a - 0) si f(a + 0)(adica limitele la stanga si la dreapta in a) exista si sunt finite, a se numeste punct de discontinuitate de speta I al functiei f; numim puncte de discontinuitate de speta II ale functiei f toate celelalte puncte de discontinuitate.
Fie f:(D\{a}) - > R o functie reala de variabila reala, unde a este un punct de
acumulare al multimii D (adica in orice vecinatate a lui a se gaseste cel putin un
element din D, diferit de a).
Daca functia f are limita finita in a si
functia
definita prin
evident continua in a, se numeste prelungirea prin continuitate a functiei f in punctul a.
Functii cu proprietatea lui Darboux:
Fie f:I - > R o functie, unde I este un interval inclus in R.
Functia f are proprietatea lui Darboux pe I, daca pentru orice a, b din I, si orice
λ intre f(a) si f(b), exista xλ € (a,b), astfel incat f(xλ) = λ.
Teorema:
Orice functie continua pe un interval are proprietatea lui Darboux pe acel interval.
Teorema lui Weierstrass:
Fie intervalul [a,b] inclus in R; orice functie continua f:[a,b] - > R este marginita si isi
atinge marginile pe acest interval (adica f([a,b]) este un interval inchis si marginit).
EXERCIŢII REZOLVATE!!!!!!!!!!!!
1) Suport teoretic:
Functie continua, functie multiforma, limite laterale, operatie exceptata, regula lui l'Hospital.
Enunt:
Sa se demonstreze ca functia urmatoare este continua pe domeniul sau de definitie:
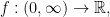

Demonstratie:
Este suficient sa se arate ca functia este continua in x = 2, adica limitele laterale in
x = 2 exista si sunt egale cu valoarea functiei in x = 2. Deci:
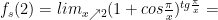
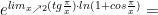

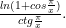
S-a obtinut operatia exceptata 0/0, se aplica, eventual, regula lui l`Hospital si se gaseste
in final ca limita la stanga in x = 2 este egala cu "e" (1).
In mod analog se procedeaza pentru limita la dreapta si se obtine tot "e" (2).
Din (1), (2) si f(2) = e (ipoteza), rezulta ca functia este continua pe domeniul sau de
definitie.
2)
Functie continua, functie multiforma, limite laterale, operatie exceptata, regula lui l'Hospital.
Enunt:
Sa se demonstreze ca functia urmatoare este continua pe domeniul sau de definitie:
Demonstratie:
Este suficient sa se arate ca functia este continua in x = 2, adica limitele laterale in
x = 2 exista si sunt egale cu valoarea functiei in x = 2. Deci:
S-a obtinut operatia exceptata 0/0, se aplica, eventual, regula lui l`Hospital si se gaseste
in final ca limita la stanga in x = 2 este egala cu "e" (1).
In mod analog se procedeaza pentru limita la dreapta si se obtine tot "e" (2).
Din (1), (2) si f(2) = e (ipoteza), rezulta ca functia este continua pe domeniul sau de
definitie.
2)
Suport teoretic:
Discontinuitate de speţa intai, functie multiforma, operatii exceptate, numarul e, regula lui L'Hospital.
Enunt:
Sa se arate ca x = π/2 este punct de discontinuitate de speţa intai pentru functia cu
acolada de mai jos:

![f(x)=\begin{cases}\frac{\sqrt[3]{cos(x+\frac{\pi}{2})}+1}{tg2x},\;{x}\in{(\frac{\pi}{4},\frac{\pi}{2})}\\0,\;x=\frac{\pi}{2}\\{(1+tg2x)}^{\frac{1}{2x-\pi}},\;{x}\in{(\frac{\pi}{2},\frac{3\pi}{4})}\end{cases}. f(x)=\begin{cases}\frac{\sqrt[3]{cos(x+\frac{\pi}{2})}+1}{tg2x},\;{x}\in{(\frac{\pi}{4},\frac{\pi}{2})}\\0,\;x=\frac{\pi}{2}\\{(1+tg2x)}^{\frac{1}{2x-\pi}},\;{x}\in{(\frac{\pi}{2},\frac{3\pi}{4})}\end{cases}.](http://s.wordpress.com/latex.php?latex=f%28x%29%3D%5Cbegin%7Bcases%7D%5Cfrac%7B%5Csqrt%5B3%5D%7Bcos%28x%2B%5Cfrac%7B%5Cpi%7D%7B2%7D%29%7D%2B1%7D%7Btg2x%7D%2C%5C%3B%7Bx%7D%5Cin%7B%28%5Cfrac%7B%5Cpi%7D%7B4%7D%2C%5Cfrac%7B%5Cpi%7D%7B2%7D%29%7D%5C%5C0%2C%5C%3Bx%3D%5Cfrac%7B%5Cpi%7D%7B2%7D%5C%5C%7B%281%2Btg2x%29%7D%5E%7B%5Cfrac%7B1%7D%7B2x-%5Cpi%7D%7D%2C%5C%3B%7Bx%7D%5Cin%7B%28%5Cfrac%7B%5Cpi%7D%7B2%7D%2C%5Cfrac%7B3%5Cpi%7D%7B4%7D%29%7D%5Cend%7Bcases%7D.&bg=FFFFFF&fg=000000&s=0)
Rezolvare:
Trebuie aratat ca limitele laterale in raport cu x = π/2 exista, sunt
finite, dar distincte.

![\frac{{cos}(x+\frac{\pi}{2})+1}{(tg2x)[\sqrt[3]{{cos}^2(x+\frac{\pi}{2})}-\sqrt[3]{{cos}(x+\frac{\pi}{2})}+1]} \frac{{cos}(x+\frac{\pi}{2})+1}{(tg2x)[\sqrt[3]{{cos}^2(x+\frac{\pi}{2})}-\sqrt[3]{{cos}(x+\frac{\pi}{2})}+1]}](http://s.wordpress.com/latex.php?latex=%5Cfrac%7B%7Bcos%7D%28x%2B%5Cfrac%7B%5Cpi%7D%7B2%7D%29%2B1%7D%7B%28tg2x%29%5B%5Csqrt%5B3%5D%7B%7Bcos%7D%5E2%28x%2B%5Cfrac%7B%5Cpi%7D%7B2%7D%29%7D-%5Csqrt%5B3%5D%7B%7Bcos%7D%28x%2B%5Cfrac%7B%5Cpi%7D%7B2%7D%29%7D%2B1%5D%7D&bg=FFFFFF&fg=000000&s=0)

x = π/2.
3) Enunt:
Fie functia f:(0,+oo) - > R, f(x) = x - lnx.
Sa se determine Imf.
Raspuns:
Imf = [1,+oo).
Rezolvare:
Se studiaza variatia functiei f cu ajutorul derivatei întâi. Deci:
f'(x) = 1 - 1/x = 0 < = > x = 1 (singurul punct critic al functiei f).
Tabelul de variatie al functiei f este:
Intrucat functia f este continuă, deducem că imaginea sa (Imf) este tot interval (ca si
domeniul sau de definitie), anume Imf = [1,+ 00].
Discontinuitate de speţa intai, functie multiforma, operatii exceptate, numarul e, regula lui L'Hospital.
Enunt:
Sa se arate ca x = π/2 este punct de discontinuitate de speţa intai pentru functia cu
acolada de mai jos:
Rezolvare:
Trebuie aratat ca limitele laterale in raport cu x = π/2 exista, sunt
finite, dar distincte.
x = π/2.
3) Enunt:
Fie functia f:(0,+oo) - > R, f(x) = x - lnx.
Sa se determine Imf.
Raspuns:
Imf = [1,+oo).
Rezolvare:
Se studiaza variatia functiei f cu ajutorul derivatei întâi. Deci:
f'(x) = 1 - 1/x = 0 < = > x = 1 (singurul punct critic al functiei f).
Tabelul de variatie al functiei f este:
| x | 0 | 1 | +oo | ||
| f'(x) | | | - - - - - | 0 | + + + + + | |
| f(x) | +oo | | 1 | | +oo |
domeniul sau de definitie), anume Imf = [1,+ 00].
Комментариев нет:
Отправить комментарий